
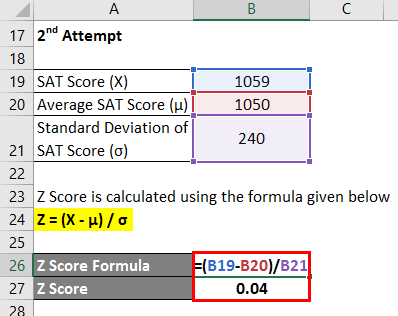
When you have multiple samples and want to describe the standard deviation of those sample means ( the standard error), you would use this z score formula: Z Score Formula: Standard Error of the Mean However, the steps for solving it are exactly the same. This is exactly the same formula as z = x – μ / σ, except that x̄ (the sample mean) is used instead of μ (the population mean) and s (the sample standard deviation) is used instead of σ (the population standard deviation). You may also see the z score formula shown to the left. In this example, your score is 1.6 standard deviations above the mean. The z score tells you how many standard deviations from the mean your score is. Assuming a normal distribution, your z score would be: The test has a mean (μ) of 150 and a standard deviation (σ) of 25. The basic z score formula for a sample is:įor example, let’s say you have a test score of 190. Z Score Formulas The Z Score Formula: One Sample A z-score can tell you where that person’s weight is compared to the average population’s mean weight.īack to Top 2. For example, knowing that someone’s weight is 150 pounds might be good information, but if you want to compare it to the “ average” person’s weight, looking at a vast table of data can be overwhelming (especially if some weights are recorded in kilograms). Results from tests or surveys have thousands of possible results and units those results can often seem meaningless. Z-scores are a way to compare results to a “normal” population. In order to use a z-score, you need to know the mean μ and also the population standard deviation σ.

Z-scores range from -3 standard deviations (which would fall to the far left of the normal distribution curve) up to +3 standard deviations (which would fall to the far right of the normal distribution curve). But more technically it’s a measure of how many standard deviations below or above the population mean a raw score is.Ī z-score can be placed on a normal distribution curve. To find the probability of LARGER z-score, which is the probability of observing a value greater than x (the area under the curve to the RIGHT of x), type: =1 - NORMSDIST (and input the z-score you calculated).Simply put, a z-score (also called a standard score) gives you an idea of how far from the mean a data point is. Then, to calculate the probability for a SMALLER z-score, which is the probability of observing a value less than x (the area under the curve to the LEFT of x), type the following into a blank cell: = NORMSDIST( and input the z-score you calculated). To make things easier, instead of writing the mean and SD values in the formula you could use the cell values corresponding to these values. Now to calculate the z-score type the following formula in an empty cell: = (x – mean) /. For example, if the range of scores in your sample begin at cell A1 and end at cell A20, the formula = STDEV.S (A1:A20) returns the standard deviation of those numbers. Next, you mush calculate the standard deviation of the sample by using the STDEV.S formula. To calculate the z-score of a specific value, x, first you must calculate the mean of the sample by using the AVERAGE formula.įor example, if the range of scores in your sample begin at cell A1 and end at cell A20, the formula =AVERAGE(A1:A20) returns the average of those numbers. If there is less than a 5% chance of a raw score being selected randomly, then this is a statistically significant result. The probability of randomly selecting a score between -1.96 and +1.96 standard deviations from the mean is 95% (see Fig. Proportion of a standard normal distribution (SND) in percentages. For example, there is a 68% probability of randomly selecting a score between -1 and +1 standard deviations from the mean (see Fig. The SND allows researchers to calculate the probability of randomly obtaining a score from the distribution (i.e.

Therefore, one standard deviation of the raw score (whatever raw value this is) converts into 1 z-score unit. The standard deviation of any SND always = 1.For example, if the distribution of raw scores if normally distributed, so is the distribution of z-scores. z-distribution) is always the same shape as the raw score distribution.


 0 kommentar(er)
0 kommentar(er)
